持久、短暂设计状况 N≤Nu (F.1.1-1)
地震设计状况 N≤Nu／γRE (F.1.1-2)
式中：N——轴向压力设计值；
Nu——钢管混凝土单肢柱的轴向受压承载力设计值。
F.1.2 钢管混凝土单肢柱的轴向受压承载力设计值应按下列公式计算：
条文说明 F.1 构件设计
F.1.1 本规程对圆型钢管混凝土柱承载力的计算采用基于实验的极限平衡理论，参见蔡绍怀著《现代钢管混凝土结构》(人民交通出版社，北京，2003)，其主要特点是：
1)不以柱的某一临界截面作为考察对象，而以整长的钢管混凝土柱，即所谓单元柱，作为考察对象，视之为结构体系的基本元件。
2)应用极限平衡理论中的广义应力和广义应变概念，在试验观察的基础上，直接探讨单元柱在轴力N和柱端弯矩M这两个广义力共同作用下的广义屈服条件。
本规程将长径比L／D不大于4的钢管混凝土柱定义为短柱，可忽略其受压极限状态的压曲效应(即P-δ效应)影响，其轴心受压的破坏荷载(最大荷载)记为N0，是钢管混凝土柱承载力计算的基础。
短柱轴心受压极限承载力凡的计算公式(F.1.2-2)、(F.1.2-3)系在总结国内外约480个试验资料的基础上，用极限平衡法导得的。试验结果和理论分析表明，该公式对于(a)钢管与核心混凝土同时受载，(b)仅核心混凝土直接受载，(c)钢管在弹性极限内预先受载，然后再与核心混凝土共同受载等加载方式均适用。
公式(F.1.2-2)、(F.1.2-3)右端的系数0.9，是参照现行国家标准《混凝土结构设计规范》GB 50010，为提高包括螺旋箍筋柱在内的各种钢筋混凝土受压构件的安全度而引入的附加系数。
公式(F.1.2-1)的双系数乘积规律是根据中国建筑科学研究院的系列试验结果确定的。经用国内外大量试验结果(约360个)复核，证明该公式与试验结果符合良好。在压弯柱的承载力计算中，采用该公式后，可避免求解M—N相关方程，从而使计算大为简化，用双系数表达的承载力变化规律也更为直观。值得强调指出，套箍效应使钢管混凝土柱的承载力较普通钢筋混凝土柱有大幅度提高(可达30％～50％)，相应地，在使用荷载下的材料使用应力也有同样幅度的提高。经试验观察和理论分析证明，在规程规定的套箍指标θ不大于3和规程所设置的安全度水平内，钢管混凝土柱在使用荷载下仍然处于弹性工作阶段，符合极限状态设计原则的基本要求，不会影响其使用质量。
F.1.3 由极限平衡理论可知，钢管混凝土标准单元柱在轴力N和端弯矩M共同作用下的广义屈服条件，在M—N直角坐标系中是一条外凸曲线，并可足够精确地简化为两条直线AB和BC(图18)。其中A为轴心受压；C为纯弯受力状态，由试验数据
F.1.4 规程公式(F.1.4-1)是总结国内外大量试验结果(约340个)得出的经验公式。对于普通混凝土，L0／D≤50在的范围内，对于高强混凝土，在L0／D≤20的范围内，该公式的计算值与试验实测值均符合良好(图22、23)。从现有的试验数据看，钢管径厚比D／t，钢材品种以及混凝土强度等级或套箍指标等的变化，对φl值的影响无明显规律，其变化幅度都在试验结果的离散程度以内，故公式中对这些因素都不予考虑。为合理地发挥钢管混凝土抗压承载能力的优势，本规程对柱的长径比作了
F.1.5、F.1.6 本条的等效计算长度考虑了柱端约束条件(转动和侧移)和沿柱身弯矩分布梯度等因素对柱承载力的影响。
柱端约束条件的影响，借引入“计算长度”的办法予以考虑，与现行国家标准《钢结构设计规范》GB 50017所采用的办法完全相同。
为考虑沿柱身弯矩分布梯度的影响，在实用上可采用等效标准单元柱的办法予以考虑。即将各种一次弯矩分布图不为矩形的两端铰支柱以及悬臂柱等非标准柱转换为具有相同承载力的一次弯矩分布图呈矩形的等效标准柱。我国现行国家标准《钢结构设计规范》GB 50017和国外的一些结构设计规范，例如美国ACI混凝土结构规范，采用的是等效弯矩法，即将非标准柱的较大端弯矩予以缩减，取等效弯矩系数c不大于1，相应的柱长保持不变(图24a)；本规程采用的则是等效长度法，即将非标准柱的长度予以缩减，取等效长度系数k不大于1，相应的柱端较大弯矩M2保持不变(图24b)。两种处理办法的效果应该是相同的。
本规程采用等效长度法，在概念上更为直观，对于在实验中观察到的双曲压弯下的零挠度点漂移现象，更易于解释。
本条所列的等效长度系数公式，是根据中国建筑科学研究院专门的试验结果建立的经验公式。
F.1.7 虽然钢管混凝土柱的优势在抗压，只宜作受压构件，但在个别特殊工况下，钢管混凝土柱也可能有处于拉弯状态的时候。为验算这种工况下的安全性，本规程假定钢管混凝土柱的N—M曲线在拉弯区为直线，给出了以钢管混凝土纯弯状态和轴心受拉状态时的承载力为基础的相关公式，其中纯弯承载力与压弯公式中的纯弯承载力相同，轴心受拉承载力仅考虑钢管的作用。
F.1.8、F.1.9 钢管混凝土中的钢管，是一种特殊形式的配筋，系三维连续的配筋场，既是纵筋，又是横向箍筋，无论构件受到压、拉、弯、剪、扭等何种作用，钢管均可随着应变场的变化而自行调节变换其配筋功能。一般情况下，钢管混凝土柱主要受压弯作用，在按压弯构件确定了柱的钢管规格和套箍指标后，其抗剪配筋场亦相应确定，无须像普通钢筋混凝土构件那样另做抗剪配筋设计。以往的试验观察表明，钢管混凝土柱在剪跨柱径比a／D大于2时，都是弯曲型破坏。在一般建筑工程中的钢管混凝土框架柱，其高度与柱径之比(即剪跨柱径比)大都在3以上，横向抗剪问题不突出。在某些情况下，例如钢管混凝土柱之间设有斜撑的节点处，大跨重载梁的梁柱节点区等，仍可能出现影响设计的钢管混凝土小剪跨抗剪问题。为解决这一问题，中国建筑科学研究院进行了专门的抗剪试验研究，本条的计算公式(F.1.9—1)和(F.1.9—2)即系根据这批试验结果提出的，适用于横向剪力以压力方式作用于钢管外壁的情况。
F.1.10～F.1.12 众所周知，对混凝土配置螺旋箍筋或横向方格钢筋网片，形成所谓套箍混凝土，可显著提高混凝土的局部承压强度。钢管混凝土是一种特殊形式的套箍混凝土，其钢管具有类似螺旋箍筋的功能，显然也应具有较高的局部承压强度。钢管混凝土的局部承压可分为中央部位的局部承压和组合界面附近的局部承压两类。中国建筑科学研究院的试验研究表明，在上述两类局部承压下的钢管混凝土强度提高系数亦服从与面积比的平方根成线性关系的规律。
第F.1.12条的公式可用于抗剪连接件的承载力计算，其中所指的柔性抗剪连接件包括节点构造中采用的内加强环、环形隔板、钢筋环和焊钉等。至于内衬管段和穿心牛腿(承重销)则应视为刚性抗剪连接件。
当局压强度不足时，可将局压区段管壁加厚予以补强，这比局部配置螺旋箍筋更简便些。局压区段的长度可取为钢管直径的1.5倍。
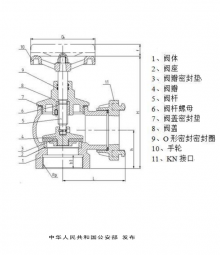室内消火栓 GB3445-20
